Table of Contents

Why Shaders Turn Black: negatives in pow() and sqrt()

Black pixels appearing in a shader often trace back to a mathematical domain error. The most common sources are the sqrt() and pow() functions when they receive invalid inputs.

In GLSL, sqrt(x) is undefined if x is negative. Similarly, pow(x, y) is undefined if x is negative and y is not an integer. When asked to perform an undefined operation, most GPUs return NaN (Not a Number). Any further math involving this NaN also results in NaN, and the renderer typically draws these pixels as black. To make matters worse, compilers often won't warn you about this potential problem, making the bug difficult to trace in a complex shader.

Visualizing the Error and the Fix

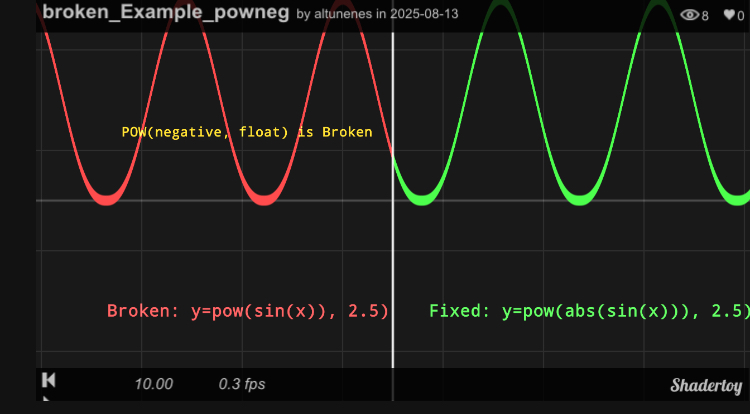
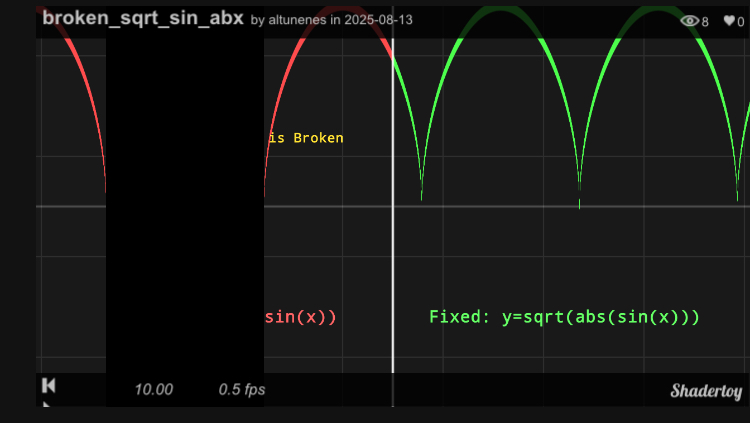
The following demos show the problem in action. The left side (red) performs the math naively. The right side (green) uses abs() to prevent errors.

1. The sqrt() Domain Error

Graphing y = sqrt(sin(x)). The gaps on the left show where sin(x) is negative and the math fails.

2. The pow() Domain Error

Graphing y = pow(sin(x), 2.5). The same issue occurs, breaking the function where the base is negative.

The Technical Reality Behind the Error

Using abs() fixes the black pixels, but it's crucial to understand why the failure occurs to write better code.

GPUs don't calculate powers through repeated multiplication. For performance, they use the mathematical identity: pow(x, y) = exp2(y * log2(x))(see ref). The failure point is log2(x). The logarithm of a negative number is undefined in the real number system. Therefore, any negative x passed to pow() causes the internal calculation to fail and produce a NaN.

While abs() prevents NaNs, it can introduce silent mathematical bugs. Consider (-2)³, which should be -8.

• pow(-2.0, 3.0) might fail due to the log/exp implementation.
• pow(abs(-2.0), 3.0) will incorrectly return 8.

This error can invert lighting or break procedural patterns. When you need to preserve the sign for odd integer powers, the correct pattern is:

float result = pow(abs(x), y) * sign(x);

A conditional check like if (x >= 0.0) might seem safe, but it's a performance trap. Branches cause 'thread divergence' on GPUs, hurting the parallelism that makes them fast. Branchless functions like abs(), max(), and sign() are far more efficient (see: theorangeduck, See: 3). Writing robust shader code means handling these cases smartly. For integer powers, explicit multiplication like x*x is always better than pow(x, 2.0) [1,2]. It's faster and avoids the log/exp path entirely. To prevent floating-point errors from creating negative inputs later, proactively clamp values with max(value, 0.0) or saturate(value), especially after operations like dot(). Finally, use abs() with care. It's a tool for getting a magnitude, not a universal patch. If you need to preserve a negative sign with an odd power, the sign(x) * pow(abs(x), y) pattern is the mathematically correct approach.

References

[1] Khronos Forums Discussion: "Pow(x, 2) different then x*x?"

[2] Register pressure in AMD CDNA2™ GPUs

[3] ADVANCED SHADER PROGRAMMING ON GCN